Cuando dos ondas que se propagan en sentidos opuestos interfieren, se produce una situación muy curiosa: la onda resultante tiene una amplitud que varía de punto a punto, pero cada uno de los puntos oscila con MAS, y en fase con los demás, dando lugar a lo que se conoce como ondas estacionarias.

Las ondas estacionarias pueden observarse en una cuerda sujeta por ambos extremos en la que se produce una vibración. La onda que viaja hacia la derecha se encuentra con la que se refleja en el extremo fijo y se produce la interferencia de ambas.

La cuerda que se ve en el vídeo se  hace vibrar mediante un dispositivo muy corriente en los laboratorios escolares (frecuencia = 50 Hz).

No todas las ondas son posibles, ya que aquellas que no tengan un nodo en los extremos están prohibidas. Existe, por tanto, una restricción física (condición de contorno): la longitud de la cuerda tiene que ser un múltiplo entero de una semilongitud de onda:

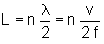
La velocidad a la que la onda se propaga por la cuerda depende de la densidad lineal de ésta (m) y de su tensión (T):

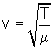
Combinando ambas expresiones obtenemos una tercera que nos da la tensión que debe tener la cuerda para que se formen las ondas permitidas:

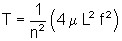
Así:

 Clic en la imagen para ver el vídeo.

Como puede verse, las ondas se forman cuando la cuerda se somete a las tensiones predichas por las ecuaciones de la izquierda, lo que se consigue regulando la masa de la pesas que la mantienen tensa.

La densidad lineal de la cuerda es 0,55 g/m.

Aunque en esta experiencia se ha mantenido constante la longitud y se varía la tensión, también pueden conseguirse ondas estacionarias variando la longitud de la cuerda y dejando inalterada su tensión.

NOTA

No hay acuerdo en la denominación de los distintos modos de vibración de una cuerda. La mayoría de los textos optan por denominar al primer modo de vibración (n=1) con el nombre de modo fundamental o primer armónico. El segundo modo de vibración (n=2) sería entonces el segundo armónico. Para n =3 aparecería el tercer armónico... etc.

No obstante, en otros textos se encuentra que al primer modo de vibración (n=1) se le da el nombre de modo fundamental. Al segundo modo de vibración (n=2) se le denomina ahora primer armónico. Para n=3 tendríamos el segundo armónico... etc.