|
|
|
|
|
El reto era intentar
reproducir el experimento (ligeramente
modificado) que permitió a Eratósotenes,
hace aproximadamente 2.250 años, medir el
radio de la Tierra.
Ver
experimento de Eratóstenes
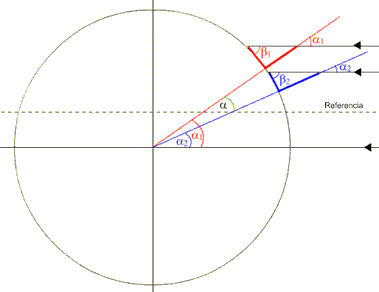
En síntesis la idea es la
siguiente (ver figura):
-
Supongamos que ponemos una
referencia (en nuestro caso el paralelo 400
N) y que determinamos la distancia de dos
puntos a dicho paralelo (se puede usar un
buen atlas o Google Earth). Restando ambas
distancias obtendríamos la distancia entre
los dos puntos considerados.
-
Si clavamos un palo vertical
(gnomon)en cada punto el sol
proyectará una sombra que formará un cierto
ángulo, mayor cuanto más al sur esté situado
el punto.
Dicho ángulo nos da la
altura del Sol sobre el horizonte del lugar.
|

Clic en la imagen para ver el
vídeo |
|
|
-
La altura del Sol va variando
a lo largo del día. Por la mañana, cuando
sale por el Este, está muy bajo, por lo que
la sombra proyectada por el gnomon será muy
larga a primeras horas de la mañana. A
medida que avanza el día, el Sol está cada
vez más alto y la sombra, en consecuencia,
se irá acortando.
-
El Sol alcanza su punto más
alto cuando pasa por
el meridiano del lugar. A ese instante se la
llama mediodía local, y para los
lugares que están situados sobre el
meridiano de Greenwich sucede a las 12:00 h
(tiempo universal o UT)
-
Por los lugares que estén
situados más al oeste, por ejemplo, el Sol
pasa más tarde por su meridiano.
Aproximadamente hay que sumar 4 min. por
cada grado de diferencia con el meridiano
de Greenwich.
|
-
Una manera de determinar el
paso del Sol por el meridiano de un lugar
(o sea la hora del mediodía local) es
obtener datos de la longitud de la sombra
arrojada por un gnomon. El instante en el
que ésta sea más corta se corresponderá
con el mediodía local.
-
Si dos observadores
calculan la altura del Sol al mediodía (a
su mediodía) la situación será similar a
la que se muestra en la figura y podremos
establecer las siguientes relaciones:
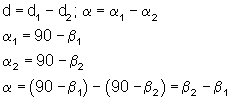
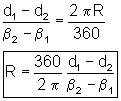
|
 |
|
 |
|
 |
Como se ve se necesitan dos
datos de cada "observatorio": la altura
del Sol al mediodía local y la distancia al
paralelo 40.
Los datos obtenidos por el
IES Juan A. Suanzes han sido los
siguientes:
-
Hora del tránsito del Sol
por el meridiano (mediodía): 12:30 h
(UT).
-
Altura del Sol al mediodía:
48,860
-
Distancia al paralelo 40:
394,5 km.
Nos hemos permitido hacer
un cálculo combinando nuestros
datos con los del IES Almunia, de Jerez de
la Frontera (Cádiz), que se encuentra en el
mismo meridiano. Los datos aportados por
este centro son:
-
Hora del tránsito del Sol
por el meridiano (mediodía): 12:30 h (UT)
-
Altura del Sol al mediodía:
55,700
-
Distancia al paralelo 40: -
369,2 km. (El signo menos indica que está
situado al sur del paralelo 40)
|
|
|
Aplicando la ecuación
deducida más arriba, tenemos:
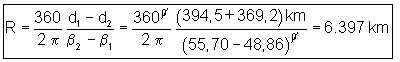
Considerando que el valor
admitido para el radio de la Tierra es de
6.371 km. el valor obtenido es de una
exactitud asombrosa.
Más información:
|
|
|
|
|